|
This course is taught since 2007 as a part of the master program M2 "Applied Mathematics" of the University of Orleans (France)
which is delocalized in the National University of Natural Sciences in Ho Chi Minh City, Vietnam. The course is shared with Professor Michel
Zinsmeister who focuses on mathematical aspects of the growth processes. This half of the course presents physical aspects and applications.
The (half)course is split into three lectures, each followed by practical work with students. The basic knowledge of probabilies and basic
skills in MATLAB are required. |
 |
Lecture 1: Diffusion
The basic notions of diffusion, random walks, Brownian motion are recalled; microscopic and macroscopic descriptions
are presented, including central limit theorem, diffusion equation, heat kernel, spectral properties of the Laplace operator,
finite-difference schemes, etc.
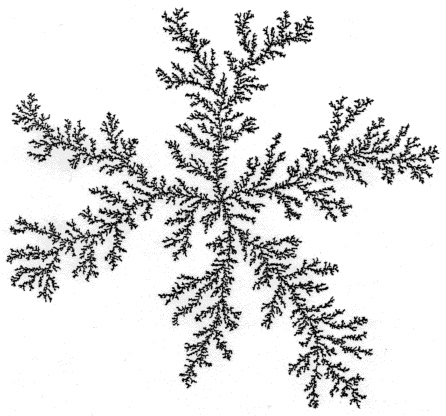
Lecture 2: Diffusive Growth Processes
The model of diffusion-limited aggregation (DLA) is presented in detail; the related mathematical notions (e.g., the harmonic
measure) are also discussed.
Lecture 3: Growth Processes in Natural Sciences
Various examples of growth processes in natural sciences are presented: morphogenesis of organs, solidification in metallurgy,
electrodeposition, instabilities in a mixture of liquids, corrosion and erosion, electric decharging (breakdown), irreversible
aggregation of colloids, formation of snowflakes, etc.
Bibliography
Growth Processes and DLA
T. Vicsek, Fractal Growth Phenomena, 2nd ed. (Singapore, World Scientific, 1992).
T. C. Halsey, Diffusion-limited aggregation: A model for pattern formation, Physics Today 53, 36-41 (2000).
T. A. Witten, L. M. Sander, Diffusion-Limited Aggregation, a Kinetic Critical Phenomenon, Phys. Rev. Lett. 47, 1400 (1981).
T. A. Witten, L. M. Sander, Diffusion-limited aggregation, Phys. Rev. B 27, 5686 (1983).
P. Bak, C. Tang, K. Wiesenfeld, Self-Organized Criticality: An Explanation of 1/f Noise, Phys. Rev. Lett. 59, 381 (1987).
J. S. Langer, Instabilities and pattern formation in crystal growth, Rev. Mod. Phys. 52, 1 (1980).
M. C. Cross, P. C. Hohenberg, Pattern formation outside of equilibrium, Rev. Mod. Phys. 65, 851 (1993).
A. J. Koch, H. Meinhardt, Biological pattern formation - from basic mechanisms to complex structures, Rev. Mod. Phys. 66, 1481 (1994).
C. Bowman, A. C. Newell, Natural patterns and wavelets, Rev. Mod. Phys. 70, 289 (1998).
J. P. Gollub, J. S. Langer, Pattern formation in nonequilibrium physics, Rev. Mod. Phys. 71, S396 (1999).
P. Meakin, The structure of two-dimensional Witten-Sander aggregates, J. Phys. A 18, L661 (1985).
P. Ossadnik, Multiscaling Analysis of Large-Scale Off-Lattice DLA, Physica A 176, 454 (1991).
General
B. Mandelbrot, The Fractal Geometry of Nature (San Francisco, Freeman, 1982)
P. Levy, Processus stochastiques et movement brownien (Paris, Gauthier-Villard, 1965)
W. Feller, An Introduction to Probability Theory and Its Applications, Volumes I and II,
Second Edition (John Wiley & Sons, New York, 1971).
F. Spitzer, Principles of Random Walk (New York: Springer, 1976)
G. H. Weiss, Aspects and Applications of the Random Walk (North-Holland, Amsterdam, 1994).
S. Redner, A Guide to First-Passage Processes (Cambridge University Press, Cambridge, England, 2001).
H. S. Carslaw, J. C. Jaeger, Conduction of Heat in Solids, 2nd Ed. (Clarendon, Oxford, 1959)
J. Crank, The Mathematics of Diffusion, 2nd Ed. (Clarendon, Oxford, 1975).
M. Freidlin, Functional Integration and Partial Differential Equations,
Annals of Mathematics Studies (Princeton University, Princeton, New Jersey, 1985).
R. F. Bass, Diffusions and Elliptic Operators (Springer, 1998).
D. S. Grebenkov, NMR Survey of Reflected Brownian Motion, Rev. Mod. Phys. 79, 1077-1137 (2007).
K. K. Sabelfeld, Monte Carlo Methods in Boundary Value Problems (Springer-Verlag: New York - Heidelberg, Berlin, 1991).
K. K. Sabelfeld and N. A. Simonov, Random Walks on Boundary for Solving PDEs (Utrecht, The Netherlands, 1994).
G. N. Milshtein, Numerical Integration of Stochastic Differential Equations (Kluwer, Dordrecht, the Netherlands, 1995).
MATLAB Initiating Courses
Basic Concepts in Matlab, by M. G. Kay
CTM: Matlab Basics Tutorial
Matlab Summary and Tutorial
Crash course in MATLAB, by T. A. Driscoll
Your appreciation can be sent to denis.grebenkov@polytechnique.edu
Last modified 07/12/2011


