DIFFUSIVE MODEL

        The basic concept of Banding Cycle under diffusive growth conditions is illustrated in Fig. 7. According to this model [6], if a melt is solidified from an initially homogeneous composition C₀, initially the a phase will form and grow, and will tend to approach steady-state condition corresponding to the a-solidus temperature of the alloy. However, before reaching the steady state, the peritectic b-phase will nucleate when the a-liquidus line intersects the undercooling line for the b-phase nucleation. If the b-nucleus is assumed to spread faster in the lateral direction compared to the normal growth of the primary a-phase, then a band of b-phase forms. The solid and liquid compositions at the interface will now vary along the solidus and liquidus lines of b-L equilibrium and tend to approach the steady state solid composition, C₀, at the b-solidus temperature. But, before reaching the steady state, the primary a -phase may again nucleate on the solid-liquid boundary of the b phase when the b liquidus line intersects the undercooling line for the a-phase nucleation. This cycle of alternate nucleation and growth of primary and secondary phases may continue leading to alternate bands of a and b . The major predictions of this diffusive banding model are: (a) the banding cycle will operate below and above the peritectic temperature, and (b) the banding window exists only for a narrow composition range.

        In the above model of discrete band formation, it was assumed that the nuclei of the new phase spread rapidly. However, this is generally not valid and one must consider the relative rates of spreading of the new phase and the continuing growth of the parent phase. The microstructrure for this complicated case was investigated by numerical simulation of a fully dynamical phase-field model of peritectic solidification for a generic peritectic phase diagram [37]. The equations of the model were simulated in a rectangular geometry with only a vertical temperature gradient. The microstructure was studied as a function of the width, L, of the sample (analogous to the sample diameter in the experiments), the composition C₀ inside the hypoperitectic region, measured here by the equilibrium volume fraction of the peritectic phase h_b which varies between zero and one inside this region, and the nucleation undercoolings of the two phases, which are normalized here by m_aDC, where m_a is the slope of the a-liquidus at the peritectic temperature and DC = C_p - C_a is the concentration jump at the a-liquid interface at this temperature. Nucleation was handled by introducing a single critical nucleus at one wall of the sample.

The simulation results summarized in Fig. 8 show that, below a minimum sample size, L_min, discrete bands of peritectic phase only fill the sample partially, thereby forming "islands" of this phase, whereas above this minimum they span its entire cross-section. The existence of this minimum size can be understood by noting that partial bands should be formed when the time for the excess solute rejected by the parent phase to diffuse across the sample is shorter than the time for the peritectic phase to spread across the sample. Since these two times are proportional to ~ L²/D and L/v_s, respectively, where v_s is the lateral spreading velocity of the peritectic phase on the parent phase, equating them yields the estimate L_min ~ D/ v_s.

Fig. 8. Different two phase microstructures predicted by the phase-field model under diffusive growth conditions in small samples.

The above estimate contains only one part of the physical mechanism that controls the transition from islands to bands. In particular, our numerical results show that L_min is a function of composition (dashed line in Fig. 9) and becomes infinite at a minimum critical composition that decreases with increasing nucleation undercooling of the peritectic phase. Below this critical composition b islands form no matter how wide is the sample. The existence of this minimum composition can be understood by noting that mass conservation implies that the b phase acts as an "impurity sink" that depletes the boundary layer of solute ahead of the growing a-phase at a rate propoortional to 1 - h_b. Hence for h_b sufficiently small, this sink effect can become large enough to overcome the driving force for the b-phase to spread laterally, independently of the sample size.

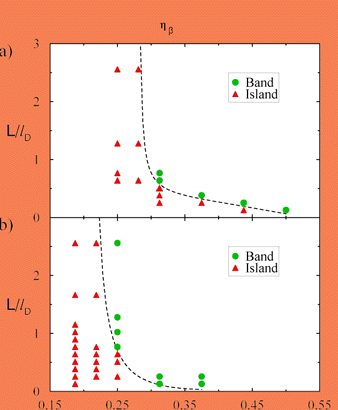
Fig. 9. Morphology diagram as a function of system size and volume fraction of the b-phase for two different nucleation undercoolings.

        We now consider the nucleation and growth of the primary phase on the peritectic phase. When the primary phase renucleates and spreads over the first band of the peritectic phase, it covers it completely only if the sample is smaller than some maximum width L_max. Fot L > L_max, the primary phase only partially fills the sample and the b phase grows continuously after the first band. In contrast to L_min, which decreaees with nucleation undercooling of the peritectic phase, L_max increases with nucleation undercooling of the primary phase. This finding can also be explained semi-quantitatively by comparing the time ~ L/V_s^a for the a-phase to traverse the sample to the time ~D/V_p² for the temperature of the a-liquid interface to fall below the peritectic temperature which yields the estimate L_max ~D V_s^a / V_p². The fact that V_s increases with DT_N^a explains our numerical finding that L_min increases with the same quantity.

        These results indicate that when only a single nucleus is allowed to form on the wall of the sample, discrete bands formation in a diffusive regime is only possible over a finite range of system sizes L_min < L < L_min. Moreover, this range depends both on the composition inside the hypoperitectic region, and the nucleation undercoolings of the two phases. For sample sizes outside this range, the microstructure consists of discrete bands of one of the two phases embedded inside the continuous matrix of the other phase, or more complex chaotic microstructures.