
 |
| Version |
| franšaise |
 |
| Russian |
| version |
|
The human placenta is a critical organ as it governs the exchange of oxygen, carbon dioxide, and nutriments of the foetus. The very complex geometrical structure of this organ requires dedicated methods for analyzing microphotographs of its cross-sections. New an efficient image processing algorithms initially designed for mineral materials have been recently developed at the Condensed Matter Physics laboratory at Ecole Polytechnique. These algorithms may now be applied to biological structures such as the human placenta in particular. The aim of this project is to study how these new algorithms may be adapted for analyzing light-microscopy images. The end goal is to automatically segment and determine types, positions, sizes and areas of different kinds of components of the human placenta such as villous trees, intervillous space, fibrinoid necrosis, foetal capillaries and trophoblast layers. The resulting data will be used in a wider international project intended to study the relationship between the morphology of the placental structure and its exchange efficiency. The student completing the project will acquire new competences image analysis, highly appreciated in modern science and industry; he also will practice and improve his programming skills in a Matlab« working environment, and will take part to an international and interdisciplinary scientific research project, at the border between physics, physiology and medicine. The candidate should possess programming skills (knowing Matlab« environment and/or C/C++ language highly recommended), basic background in computer sciences and applied mathematics and strong motivations for interdisciplinary research. |
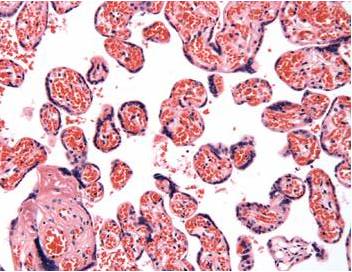
A part of a high-resolution photograph of a two-dimensional slice of the placenta (courtesy by C. Salafia) |
|
Diffusive transport in porous media is ubiquitous in biology and material sciences. For instance, the geometrical structure of a cement paste essentially determines the related physico-chemical processes and the consequent hardening and mechanical strength of the concrete. The structure of sedimentary rocks influences the oil distribution and conditions the efficiency and cost of oil recovery. In both examples, porous media exhibit a complex hierarchical network of interconnected pores of sizes ranging from nanometers to millimeters. Modern X-ray microtomography and microscopy allow one to determine the morphology of various porous media with a spatial resolution ranging from ten nanometers to several microns. Although diffusive transport in the reconstructed structures can in principle be studied numerically, their complexity and multiscale character make complete numerical simulations too time-consuming for a routine characterization of porous materials. A coarser description of diffusive transport through a decomposition of the whole structure of the medium into a network of "elementary" pores is therefore required. For instance, each elementary pore could be represented by a site of the network, while a connection between two adjacent pores could be represented by a link between two sites. Diffusion inside each pore and between two adjacent pores is effectively modeled as jumps between the sites. The two fundamental problems are: 1) how to decompose a given medium into representative elementary pores (such a decomposition is far from being unique), and 2) how to assign transition rules on a network given that pore shapes and sizes are highly inhomogeneous. Once a reliable decomposition is established, analytical and numerical studies of random walks on networks can be undertaken. The rapidity of random walk algorithms should allow one for investigating diffusive transport in the whole sample at macroscopic time and length scales. The PhD thesis aims at developing these ideas through numerical simulations in model and realistic porous media encountered in the fields of catalysis, oil recovery and building materials. At first step, an off-lattice Monte Carlo algorithm will be implemented for simulating restricted diffusion in model shapes such as minimal surfaces, vycor pore glasses, etc. Bearing in mind oil-recovery applications, a special focus will be on models in which the geometry can be continuously varied from connected to disconnected configurations. The numerical simulations will allow us to determine the first-exit time statistics that answer the question: How long does it take for a diffusing particle started inside a pore to reach some parts of the pore boundary? The exit probability and the mean exit time will then be used to formulate the transition matrix and waiting times for random walks on the pore network. Once a reliable network representation of a porous medium is validated for model geometries, extensive numerical simulations will be started in order to investigate diffusive transport in realistic porous media. This study should allow us to give a rigorous formulation of classical notions such as "elementary pores" and "tortuosity". The numerical results can potentially be confronted with experimental measurement by pulsed-gradient spin-echo techniques also performed in the research group. The ultimate goal of the PhD thesis is to provide a reliable coarse description of diffusive transport in hierarchical porous media and to characterize it by few relevant geometry-based parameters. The candidate is expected to have a background in statistical physics and to be skilled in numerical methods and programming. |

Three-dimensional reconstructed structure of a cement paste (courtesy by V. Tariel) |
|
The mature placenta is a complex arborized vascular bed allowing for exchange between the mother and fetus. From the perspective of maternal perfusion, intervillous blood flow accesses individual terminal villi at different flow rates. Oxygen dissolved in the maternal blood diffuses across the villous membrane toward and into the fetal capillaries, from where it is carried away by fetal blood. Conversely, carbon dioxide dissolved in the fetal blood diffuses into the villus and then across the villous membrane to be carried away by the maternal blood. How does the geometry of the placental villous architecture determine the oxygen and carbon dioxide transport efficiency? In particular, does abnormal packing density of villi affect their function? In the case of abnormally dense packing (e.g., in diabetic placentas), do some villi "shield" other villi from the maternal perfusion and limit their function? In the case of abnormally sparse packing (e.g., in preeclamptic placentas), does maternal blood transit the intervillous space without oxygen transfer? How is the oxygen flux correlated with gestational age, birth weight and other perinatal outcomes? Understanding the efficiency of oxygen transport may have a crucial medical impact. The fetus has two functions before birth, to develop mature organs and to grow. Both these functions are dependent on adequate resources of oxygen exchange. While much is known about villous structures in normal and diseased placentas, only very little is known about how changes in villous structure impact villous function. In the last two decades, increasing data support a role in lifelong disease for a poor intrauterine environment. The most commonly used proxy for the adequacy of the intrauterine environment is birthweight. Risks of death at age 50 from heart disease, risks of diabetes, certain cancers as well as neurodevelopmental and neuropsychiatric disease all have been shown to vary with birthweight. Better understanding of how fetal growth is modulated by placental function that is dependent on placental structure will help clarify how birth weight changes have such far-reaching effects, and may allow early risk prediction to improve lifelong health. The project aims at studying the maternal blood flow in the intervillous space from the umbilical arteries toward terminal villi. The goals are to determine the oxygen delivery to the villous membranes, to evaluate the impact of anatomical pathologies (e.g., overcrowding of the villi in the diabetic placentas) on the spatial distribution of partial oxygen pressure, and finally to access the role of diffusion/convection screening in normal and diseased placentas. At the end, we shall be able to calculate the total flux of oxygen from the mother to the fetus and to understand the consequences of placental diseases on the fetus, and to relate this quantity to the birthweight and other perinatal outcomes. The candidate is expected to have a background in physics of diffusion/convection transport, to be skilled in numerical methods and programming, and strongly motivated to work in a cross-disciplinary project with applications in physiology and medicine. The internship can eventually be continued a PhD thesis. |

A part of a high-resolution photograph of a two-dimensional slice of the placenta (courtesy by C. Salafia) |
|
The price development of assets on financial markets are determined by the superposition of the actions of market participants creating offer and demand for a financial asset. The resulting price time series exhibit significant autocorrelations for very small intra day scales and a "fat-tailed" distribution of asset returns. Memory effects and non-Gaussian features of price time series are of great importance for automated trading, especially for high-frequency trading. Fractional Brownian motion and Levy processes are now classical models that may partly account for these features. Recently, an alternative, statistical-physics-oriented approach was proposed [1,2]. This approach consists in simulating an order book, in which many agents trade one asset at a virtual exchange. Depending on the current asset price, each agent can randomly choose to buy or cell the asset according to simple probabilistic rules. This action determines the new price. In this way, the asset price time series is generated. The internship aims at studying multi-agent-based order book models and their applicabity for generating futures price series. After implementation of the model, the generated time series have to be statistically analyzed and compared to futures historical data. The goal is to determine the appropriate probabilistic rules for agents that would reproduce the main features of historical price series. |
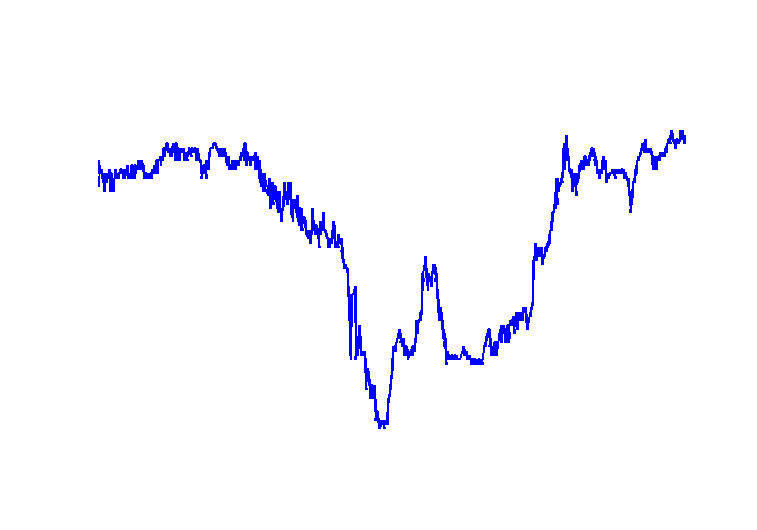
Price variation of an asset during one day |
|
Water, oxygen, nutrients and metabolites are transported to and from cells across the capillary wall and through the interstitial spaces of tissues. The interstitial space is a heterogeneous porous structure that is composed of two main phases: "solid" collagen fibers primarily supplying mechanical support of the tissue, and a fluid-rich gel providing aqueous "channels" for transport of water and solutes. Given the complexity of the interstitial geometry and the inherent difficulties in identifying its functional in vivo structure, very little is actually known about the local mechanisms mediating interstitial transport. In this project, we start with a simple geometrical model for the interstitial space considered as a pack of randomly oriented cylinders representing collagen fibers. This model of a porous medium had been studied in different contexts, in particular, in material sciences. Here we will adapt it to investigate the consequences of structural changes associated with acute injury, wound healing and chronic inflammatory and degenerative processes, by modifying key geometrical parameters. As the starting point, diffusion in a pack of cylindrical fibers will be modeled by Monte Carlo techniques, which are flexible and easily adaptable to various geometrical models. This numerical investigation should reveal how packing geometric parameters (porosity, diameter of cylinders, polydispersity, spatial distribution, etc) can affect various transport characteristics, in particular, time-dependent concentration. |
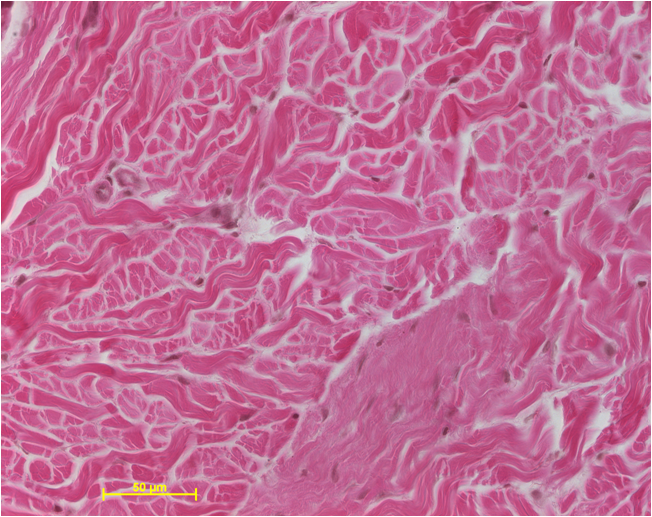
Two-dimensional slice of human skin (courtesy by M. McGee) |
|
In magnetic resonance imaging (MRI), inhomogeneous magnetic fields are applied to "encode" stochastic trajectories of the nuclei. A linear magnetic field gradient is the most usual encoding scheme, for instance, in medical imaging of the lungs. However, the nuclei usually diffuse in a bounded medium (e.g., cells or organs in biology, solid matrices in material sciences). The difference in magnetic susceptibility between the diffusing gas or liquid and its "container" induces local magnetic fields that are superimposed with externally applied linear gradients and may considerably bias the results of measurement. On the other hand, the local fields can potentially be used to enhance the image contrast. It is therefore important to understand the influence of the susceptibility-induced magnetic fields onto MRI measurements. In this project, we consider model three-dimensional labyrinths representing the lung structure. First, the spatial distribution of the susceptibility-induced magnetic field will be calculated numerically inside a given labyrinth. Second, restricted diffusion of the nuclei in this field will be simulated by a Monte Carlo technique. The numerical results can then be validated by a direct comparison with experiments. |

Kitaoka model of the human acinus |
|
Numerous transport processes in nature and industry are governed by molecular diffusion (called also Brownian motion, random walks, Wiener process, etc.). Moreover, certain biological systems exhibit branched structures as, for instance, lungs or kidney. It is therefore important to study transport processes in these systems and to understand the role of their branching structure. This problem has been largely studied in the group "Physics of Irregularity" of LPMC. In particular, we have developed a technique for analytical computation of stationary diffusion in a tree (a graph without loops) taking into account reaction/absorption [1]. The goals of the internship are
|
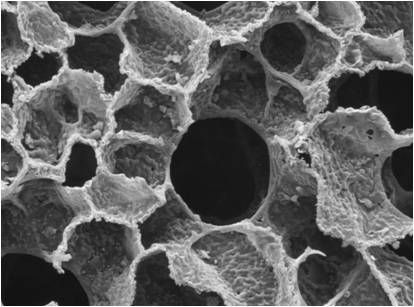
A photograph of the human acinus internal structure (courtesy by E. Weibel) |
|
Diffusive transport in complex geometries is ubiquitous in nature and industry: biochemical regulation in cells, diffusion-limited reactions in catalysis, to name a few. The interplay between geometrical complexity and stochastic character of diffusion remains poorly understood, especially in three dimensions. A spectral formulation of diffusion problems is a fundamental way to reveal the role of the geometry and to explain various striking phenomena observed in experiments. In this light, restricted diffusion in complex geometries can be investigated through the properties of the Laplace operator eigenfunctions. The first part of this project consists in a numerical computation of the eigenfunctions in several model geometries: von Koch snowflakes, random packs of disks and spheres, and 3d labyrinth structures. In the second part, the properties of these eigenfunctions have to be thoroughly investigated, in particular, an emergence of spatially localized eigenmodes and its relation to geometrical complexity. In the third part, the role of the localized eigenmodes for various diffusive phenomena has to be revealed, with special focus on nuclear magnetic resonance applications (matrix formalism). The project necessarily relies on using theoretical and numerical tools. A basic knowledge in mathematical physics, spectral analysis, probability theory and/or partial differential equations is recommended. Programming and computer skills are particularly welcome. |
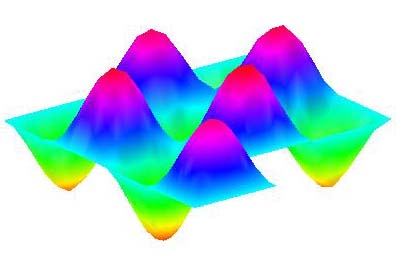
An extended eigenfunction in two connected squares |