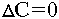
Laplacian Transport Problem
Various phenomena
There are different phenomena in physics, chemistry and biology generally called
Laplacian transfer problems , [1]:
- diffusion through semi-permeable membranes [3,4]
- electrode problem [3,4]
- heterogeneous catalysis [6]
- NMR in porous media [2]
Let us consider the diffusion of particles from the source (usually supposed planar) to the semi-permeable membrane with rather complex geometry. In the steady-state regime, the concentration of particles C obeys the Laplacian equation,
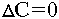
The concentration on the source is supposed to be constant.
The flux of particles through the membrane can be represented by two ways.
Near the membrane's boundary it is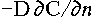 
, where D
is the diffusion coefficient. On the other hand, the membrane has finite
permeability W, therefore the flux through it's boundary is
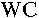. Equiling these flux, we obtain the
mixed boundary condition on the membrane's boundary
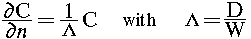
The Laplacian problem under such condition is significantly more complex than the same problem under the Dirichlet or Neumann boundary condition.
For the electrode problem, this is the electrical potential V that obeys the Laplacian equation,
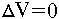
The current in the electrolyte
with resistivity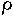 
near the complex electrode is
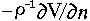. The flux of electrons through the electrode
surface is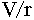 
, where r is the interface
resistivity. Thus we obtain again the mixed boundary condition,
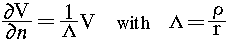
The heterogeneous catalysis and NMR in porous media have exactly the same mathematical description.
In order to solve the problem, M.Filoche and
B.Sapoval
proposed the following program [3,4]:
- to choose the appropriate discretization;
- to solve the discrete problem;
- to take the continuous limit.
They introduced the Brownian self-transport operator Q
which controls the properties of the Laplacian transfer and
depends only on the geometry of membrane's boundary.
This operator can be easily defined for a given discrete membrane:
Q(j,k) is the probability of first contact with the k-th
site of the membrane when starting from the j-th site (without
touching other sites!).
Brownian self-transport operator
The Laplacian transfer problem can be solved with the help of the Brownian self-transport operator. Thus we are engaged to study the properties of this operator.
In 1999, we considered the planar membrane given that
for this case one can calculate all characteristics
of the Laplacian transfer and of the Brownian self-transport
operator analytically. It was found that [5,6]:
- the integrated density of states does not almost
depend on the membrane's geometry, and repeats the
integrated density of states for the planar membrane
which was calculated explicitly.
- the main contribution to the spectroscopic impedance
is due to smooth eigenvectors of Q which correspond
to eigenvalues near 1. This result can be the base of
various approximations.
- the physical parameter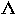 
can be viewed
as the absorption length, i.e., it defines the length
of the region which absorbs approximately a half of particles.
In 2001, we constructed explicitly the Brownian self-transport operator [8,9].
Using the technique of characteristic functions, we found the distribution of
hitting probabilities for a rather general membranes
on d-dimensional hypercubic lattice. We established
the explicit matrix equation for the Brownian self-transport
operator. It means that one can use the simple
linear algerba methods to obtain Q with a high accuracy.
Our method has different advantages:
-- possibility of analytical researches for the
general membranes;
-- simplicity and efficienty of numerical calculations;
-- study of three-dimensional membranes.