Lors de la propagation de fracture on observe la formations de structures complexes qu’il est difficile de prévoir. Afin de mieux comprendre leur formation et de montrer dans quelles mesure de telles structures peuvent s’expliquer par des lois de propagation simple nous utilisons la méthode du champ de phase pour calculer les formes de fractures tri et bi dimensionnelles lors de leur propagation dans des milieux homogènes. Cette méthode repose sur l’utilisation d’un champ auxiliaire φ continu dans l’espace qui décrit l’état du matériau (intact : φ=1 ou brisé φ=0. ). L’évolution de φ est gouvernée par une dynamique de type Ginzburg-Landau couplée à l’élasticité, ce qui permet (moyennant un choix adéquat du couplage) de décrire la propagation de fractures.
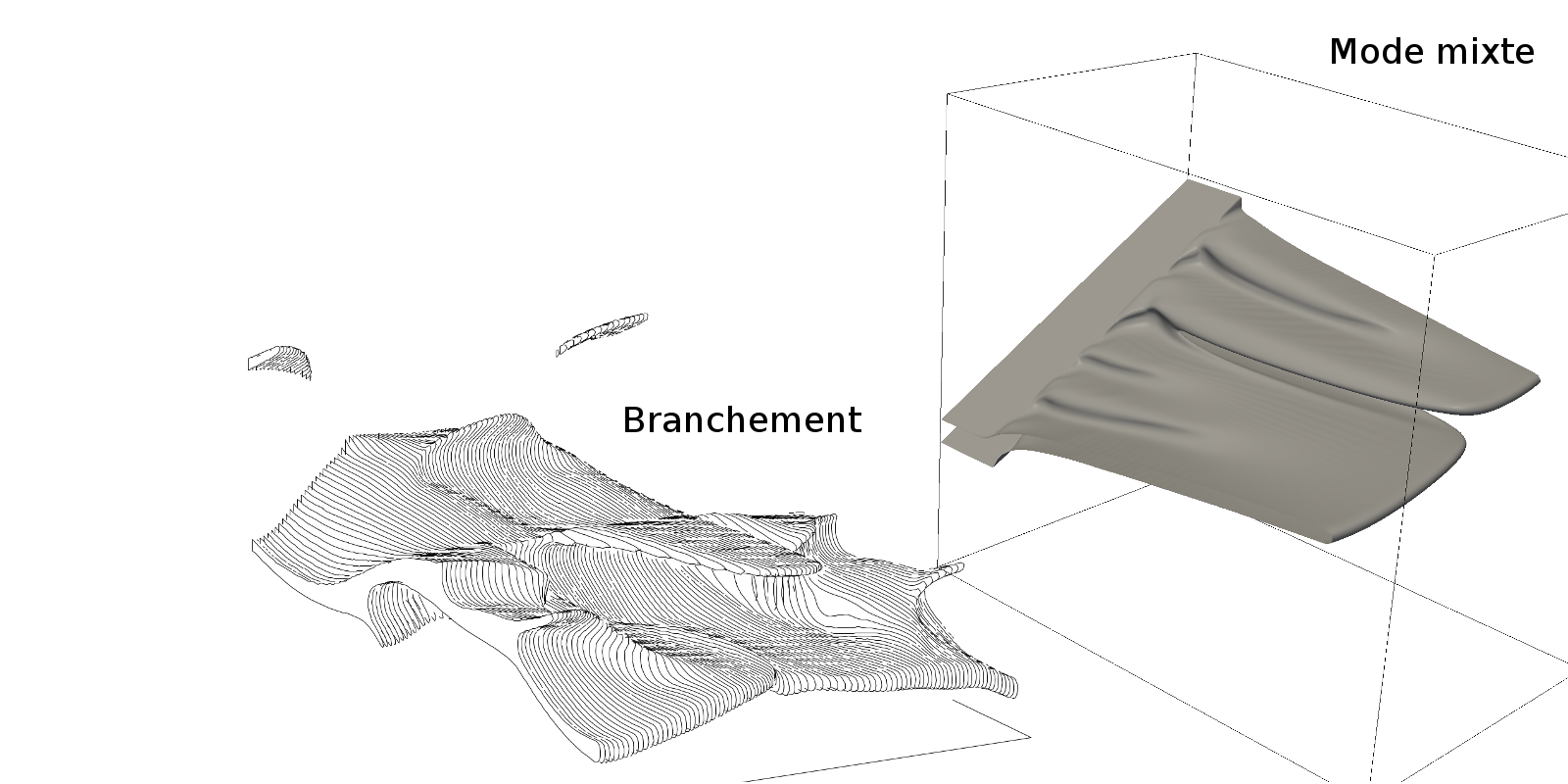
Nous avons ainsi étudié les instabilités d’un front de fissure soumis à un chargement mixte (I+III) ou l’instabilité de branchement d’un front de fissure rapide. Des images de morphologies de fractures dans ces deux cas sont représentées ci dessous.
Nous travaillons aussi à l’étude de la propagation de fractures dans les matériaux
hétérogènes.
 |
|
Images de la morphologie d’une surface de fracture (iso surface φ=0.5) obtenues lors de simulations de propagation rapide de fractures (branchement) et de propagation en mode mixte (I+III). |
References
[1]H. Henry Crack front instabilities under mixed mode loading in three dimensions EPL (Europhysics Letters), Volume 114, Number 6 Europhysics Letters ou Arxiv open access
[2]H. Henry, M. Adda-Bedia Fractographic aspects of crack branching instability using a phase field model Phys. Rev. E 88, 060401(R) (2013) Physical Review E ou
Arxiv open access

